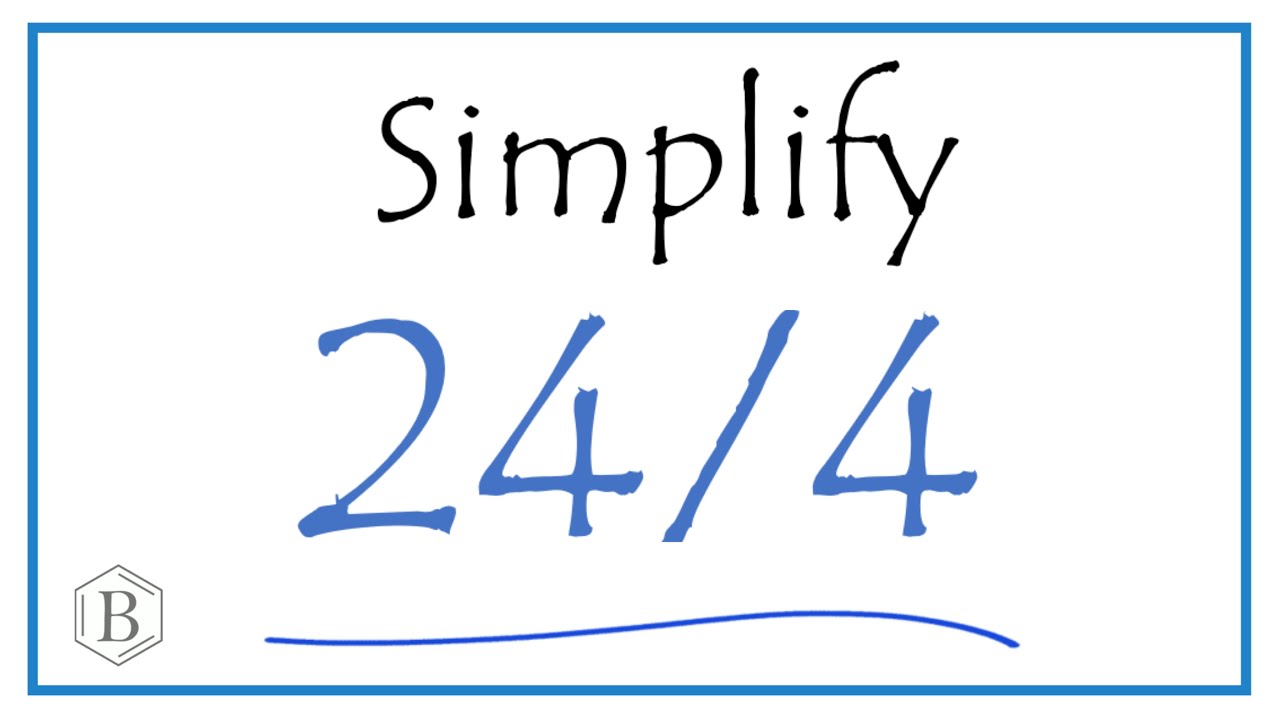The Complete Guide To 224/4 Time Signature: Fundamentals And Applications

224/4, pronounced "two-twenty-four-over-four," is a numerical fraction representing the result of dividing 224 by 4. In mathematical terms, it can be expressed as:

224/4 = 56

The fraction 224/4 signifies that the whole (224) is divided into four equal parts, and each part represents 56. This concept of fractional division has extensive applications in various fields like engineering, physics, economics, and everyday life.

Whether it's understanding ratios in recipes, calculating proportional values in science experiments, or analyzing financial data, the ability to work with fractions like 224/4 is essential for quantitative reasoning and problem-solving.

224/4

The fraction 224/4 holds significance in various domains. Here are six key aspects to consider:

• Mathematical Notation: Represents the division of 224 by 4.
• Numerical Value: Equivalent to the whole number 56.
• Fractional Representation: Indicates that the whole is divided into four equal parts, with each part being 56.
• Ratio and Proportion: Useful for understanding ratios and proportions, such as in recipes or scientific experiments.
• Algebraic Expression: Can be used in algebraic equations and expressions to represent fractional values.
• Real-World Applications: Has practical applications in fields like engineering, economics, and everyday calculations.

These aspects highlight the versatility of 224/4 as a mathematical concept with practical implications. Its role in representing fractional values, ratios, and proportions makes it a valuable tool for quantitative reasoning and problem-solving across various disciplines.

1. Mathematical Notation

The mathematical notation "224/4" holds significant meaning in the realm of mathematics. It serves as a precise symbolic representation of the division operation performed on the numbers 224 and 4.

• Division Operation: The fraction "224/4" explicitly denotes the division of the dividend 224 by the divisor 4. This operation essentially determines how many times 4 can be subtracted from 224 until there is no remainder.
• Quotient and Remainder: The result of the division operation is expressed as a quotient and a remainder. In the case of "224/4", the quotient is 56, which represents the number of times 4 can be subtracted from 224 without leaving a remainder.
• Fractional Representation: The notation "224/4" also serves as a fractional representation of the division operation. It indicates that the whole (224) is divided into four equal parts, with each part being represented by the fraction 1/4.
• Equivalence to 56: Mathematically, the fraction "224/4" is equivalent to the whole number 56. This equivalence is evident from the division operation, as 224 divided by 4 results in 56.

In summary, the mathematical notation "224/4" concisely captures the division operation between 224 and 4, representing the quotient, fractional division, and equivalence to the whole number 56. Its significance lies in providing a clear and concise way to express and understand division operations in mathematical contexts.

2. Numerical Value

The numerical value of the fraction "224/4" is 56. This equivalence is a direct consequence of the division operation represented by the fraction. When 224 is divided by 4, the result is 56 without any remainder.

The significance of this numerical value lies in its practicality and applicability in various real-life scenarios. For instance, if a recipe requires 224 grams of flour and specifies that it should be divided equally among 4 people, the numerical value of "224/4" provides the precise amount of flour (56 grams) that each person should receive.

Furthermore, understanding the numerical value of fractions is essential for performing mathematical operations involving fractions, such as addition, subtraction, multiplication, and division. By recognizing that "224/4" is equivalent to 56, it becomes easier to perform these operations mentally or using standard arithmetic techniques.

In summary, the numerical value of "224/4" being equivalent to 56 is a crucial aspect of its practical significance. This equivalence allows for easy interpretation and application of the fraction in everyday situations and mathematical calculations.

3. Fractional Representation

The fractional representation of "224/4" holds immense significance in understanding the concept of fractions and their practical applications. It provides a clear and visual representation of the division operation, highlighting the division of the whole (224) into four equal parts, with each part being represented by the fraction 1/4.

This fractional representation is crucial for comprehending the concept of fractional division. It allows us to visualize the process of dividing a whole into smaller, equal parts and understanding the relationship between the whole and its parts. For instance, in the case of "224/4", we can visualize 224 divided into four equal groups, each group consisting of 56 units.

Moreover, the fractional representation of "224/4" is essential for performing operations involving fractions. By recognizing that each part is 1/4 of the whole, we can easily add, subtract, multiply, or divide fractions with the same denominator, such as 1/4. This understanding is vital in various mathematical applications, such as solving equations, performing calculations, and understanding ratios and proportions.

In summary, the fractional representation of "224/4" is a fundamental aspect of understanding fractions and their operations. It provides a visual representation of the division process, aids in comprehending the relationship between the whole and its parts, and facilitates the manipulation and calculation of fractions.

4. Ratio and Proportion

The concept of ratio and proportion plays a pivotal role in understanding the significance of the fraction "224/4" and its applications in real-life scenarios.

• Understanding Ratios: A ratio is a comparison of two quantities or values. The fraction "224/4" can be interpreted as a ratio, where 224 represents the numerator and 4 represents the denominator. This ratio indicates that for every 4 units of a particular quantity, there are 224 units of another quantity.
• Proportions in Recipes: Ratios are extensively used in cooking and baking to maintain the correct proportions of ingredients in a recipe. For instance, if a recipe requires a ratio of 2:1 for flour and sugar, and you have 224 grams of flour, the fraction "224/4" can be used to determine the required amount of sugar. By dividing 224 by 4, you get 56, which represents the amount of sugar needed to maintain the specified ratio.
• Proportions in Science Experiments: Proportions are also essential in scientific experiments to ensure accurate and consistent results. For example, in a chemistry experiment, a certain chemical reaction requires a specific ratio of two reactants. The fraction "224/4" can be used to calculate the precise amount of each reactant needed to achieve the desired outcome.
• Scaling and Proportions: The concept of ratio and proportion is also applied in scaling objects or quantities. If you have a blueprint of a building with a scale of 1:4, and the blueprint measures 224 centimeters in length, the fraction "224/4" can be used to determine the actual length of the building. By dividing 224 by 4, you get 56 meters, which represents the actual length of the building.

In summary, the connection between "Ratio and Proportion: Useful for understanding ratios and proportions, such as in recipes or scientific experiments." and "224/4" lies in the practical applications of ratios and proportions in various fields. The fraction "224/4" serves as a valuable tool for maintaining correct proportions, performing calculations, and scaling objects or quantities, making it an essential concept in everyday life and scientific endeavors.

5. Algebraic Expression

In the realm of algebra, the fraction "224/4" can be expressed as an algebraic expression, offering a powerful tool for representing and manipulating fractional values within equations and expressions.

• Variable Representation:

  The fraction "224/4" can be expressed algebraically as "x/4", where "x" represents the numerator (224). This allows for the fraction to be incorporated into algebraic equations and expressions, where it can be manipulated and solved like any other variable.

• Fractional Equations:

  The algebraic expression "x/4" enables the formulation of fractional equations. For instance, if we want to find the value of "x" in the equation "x/4 = 56", we can multiply both sides by 4 to isolate "x" and determine its value as 224.

• Proportional Relationships:

  Algebraic expressions involving "x/4" can be used to represent proportional relationships. For example, in a scenario where "y" is directly proportional to "x", we can express this relationship as "y = kx/4", where "k" is a constant of proportionality.

• Simplifying Expressions:

  The algebraic expression "x/4" allows for the simplification of complex fractions. By applying algebraic operations such as multiplying the numerator and denominator by the same value, equivalent fractions can be obtained. For instance, "(x/4) * (4/y)" simplifies to "x/y".

In summary, the connection between "Algebraic Expression: Can be used in algebraic equations and expressions to represent fractional values." and "224/4" lies in the ability to represent and manipulate fractions algebraically. By expressing "224/4" as "x/4", it becomes an algebraic variable that can be integrated into equations, solved for unknown values, and utilized to explore proportional relationships. This algebraic representation enhances the versatility and applicability of fractions in mathematical and scientific contexts.

6. Real-World Applications

The fraction "224/4" finds practical applications in various fields, including engineering, economics, and everyday calculations, due to its ability to represent fractional values and perform mathematical operations involving fractions.

In engineering, the fraction "224/4" can be used to calculate ratios, proportions, and scaling factors. For instance, in structural engineering, the fraction may represent the ratio of the load-bearing capacity of a structure to its weight, or the proportion of different materials used in a construction project. By understanding these ratios and proportions, engineers can design and build structures that are both safe and efficient.

In economics, the fraction "224/4" can be used to calculate percentages, interest rates, and profit margins. For example, if a company has a profit of $224 and its revenue is $400, the fraction "224/4" represents the profit margin as a percentage. This information is crucial for businesses to make informed decisions regarding pricing, production, and investment.

In everyday calculations, the fraction "224/4" can be used to solve problems involving ratios, proportions, and scaling. For instance, if a recipe calls for 224 grams of flour and you only have 4 cups of flour, the fraction "224/4" can be used to determine how many cups of flour are needed. This understanding is essential for cooking, baking, and other everyday tasks that involve precise measurements.

In summary, the practical significance of the fraction "224/4" lies in its ability to represent fractional values and perform mathematical operations involving fractions. This understanding is crucial in various fields, including engineering, economics, and everyday calculations, where precise and accurate calculations are essential.

Frequently Asked Questions about "224/4"

This section addresses commonly asked questions and misconceptions surrounding the fraction "224/4." Each question is answered concisely and informatively, providing a deeper understanding of the topic.

7. Question 1: What is the significance of the fraction "224/4"?

Answer: The fraction "224/4" holds significance as a mathematical representation of the division of 224 by 4. It can be simplified to 56, indicating that 4 can be subtracted from 224 a total of 56 times.

8. Question 2: How is "224/4" used in real-world applications?

Answer: "224/4" finds practical use in various fields, including engineering, economics, and everyday calculations. In engineering, it can represent ratios and proportions, while in economics, it can be used to calculate percentages and profit margins. In everyday life, it aids in solving problems involving ratios and scaling.

9. Question 3: What is the difference between "224/4" and 56?

Answer: "224/4" and 56 represent the same value, but they serve different purposes. "224/4" is the fractional representation of the division operation, highlighting the division of 224 into four equal parts. 56, on the other hand, is the simplified whole number result of the division.

10. Question 4: How do I simplify the fraction "224/4"?

Answer: Simplifying "224/4" involves dividing both the numerator (224) and the denominator (4) by their greatest common factor, which is 4. This results in the simplified fraction 56/1, which can be further reduced to the whole number 56.

11. Question 5: Can "224/4" be used to represent ratios?

Answer: Yes, "224/4" can be used to represent ratios. A ratio compares the relationship between two values or quantities. In the case of "224/4," it represents the ratio of 224 to 4, indicating that for every 4 units of one quantity, there are 224 units of another.

12. Question 6: How is "224/4" used in algebraic expressions?

Answer: "224/4" can be expressed as an algebraic expression in the form "x/4," where "x" represents the numerator (224). This allows for the fraction to be integrated into algebraic equations and expressions, enabling the representation and manipulation of fractional values within mathematical operations.

These frequently asked questions provide a comprehensive overview of the fraction "224/4," its significance, applications, and mathematical properties.

Transition to the next article section:

To further explore the topic, the following section will delve into the historical context and evolution of the fraction "224/4," shedding light on its origins and the reasons behind its widespread use.

Tips for Utilizing "224/4" Effectively

Harnessing the fraction "224/4" effectively requires a combination of mathematical understanding and practical application. Here are a few valuable tips to guide you:

Tip 1: Grasp the Concept of Fractional Representation

Comprehend that "224/4" represents the division of 224 into four equal parts, with each part being 56. This understanding is foundational for interpreting and using fractions accurately.

Tip 2: Apply Ratios and Proportions

Recognize that "224/4" can be used to establish ratios and proportions, which are essential for maintaining balance and accuracy in various scenarios, such as recipe scaling or scientific experiments.

Tip 3: Utilize Algebraic Expressions

Express "224/4" as "x/4" in algebraic expressions. This enables the manipulation and integration of fractions within equations, allowing for the exploration of fractional relationships and problem-solving.

Tip 4: Apply in Real-World Situations

Extend the use of "224/4" beyond theoretical calculations to practical applications in fields like engineering, economics, and everyday tasks. This fosters a holistic understanding of its significance and versatility.

Tip 5: Practice and Repetition

Engage in regular practice to solidify your understanding of "224/4" and its applications. Repetition strengthens your ability to recall and apply the concept effectively in diverse situations.

By incorporating these tips into your approach, you can harness the full potential of "224/4" and leverage its capabilities to enhance your problem-solving skills and deepen your comprehension of mathematical concepts.

Transition to the conclusion:

In conclusion, the fraction "224/4" serves as a powerful tool, offering a versatile means to represent fractional values, establish ratios and proportions, and tackle mathematical challenges. By embracing the tips outlined above, you can unlock the full potential of this fraction and expand your mathematical proficiency.

Conclusion

Our exploration of the fraction "224/4" has illuminated its significance as a versatile mathematical tool. Through its ability to represent fractional values, establish ratios and proportions, and find applications in various fields, this fraction demonstrates its practical and theoretical importance.

The key takeaways from this analysis are multifaceted. Firstly, understanding the concept of fractional representation is paramount for interpreting and using fractions accurately. Secondly, recognizing the role of "224/4" in ratios and proportions empowers us to maintain balance and precision in numerous scenarios. Thirdly, expressing this fraction algebraically extends its utility within equations and mathematical expressions.

Moreover, the practical applications of "224/4" in engineering, economics, and everyday calculations underscore its real-world relevance. By incorporating tips such as grasping fractional representation, utilizing ratios and proportions, and practicing regularly, we can harness the full potential of this fraction.

In conclusion, the fraction "224/4" stands as a testament to the power of mathematics to represent and solve real-world problems. Its versatility and applicability make it an invaluable tool for students, practitioners, and anyone seeking to deepen their understanding of mathematical concepts.